Sarah is driving. Her distance in km from Tempe after t hours of driving is given by: x = D(t) = 13 + 57ta. Determine a formula in terms of x for: t = D^-1(x)b. Compute D^-1(70)c. In the expression D^-1(x) :what quantity (distance or time) does the x represent?what quantity (distance or time) does the entire D^-1(x) represent?d. Which of the following statements best describes D^-1(x)? a) the ratio of Sarah's distance from Tempe (in km) to x hours of driving. b) the reciprocal of Sarah's distance from Tempe (in km) after x hours of driving. c) the number of hours of driving needed for Sarah to be x km from Tempe. d) Sarah's distance in km from Tempe after x hours of driving.
-
Subject:
Mathematics -
Author:
brielle -
Created:
1 year ago
Answers 2
Answer:
The solutions for your four question problem are:
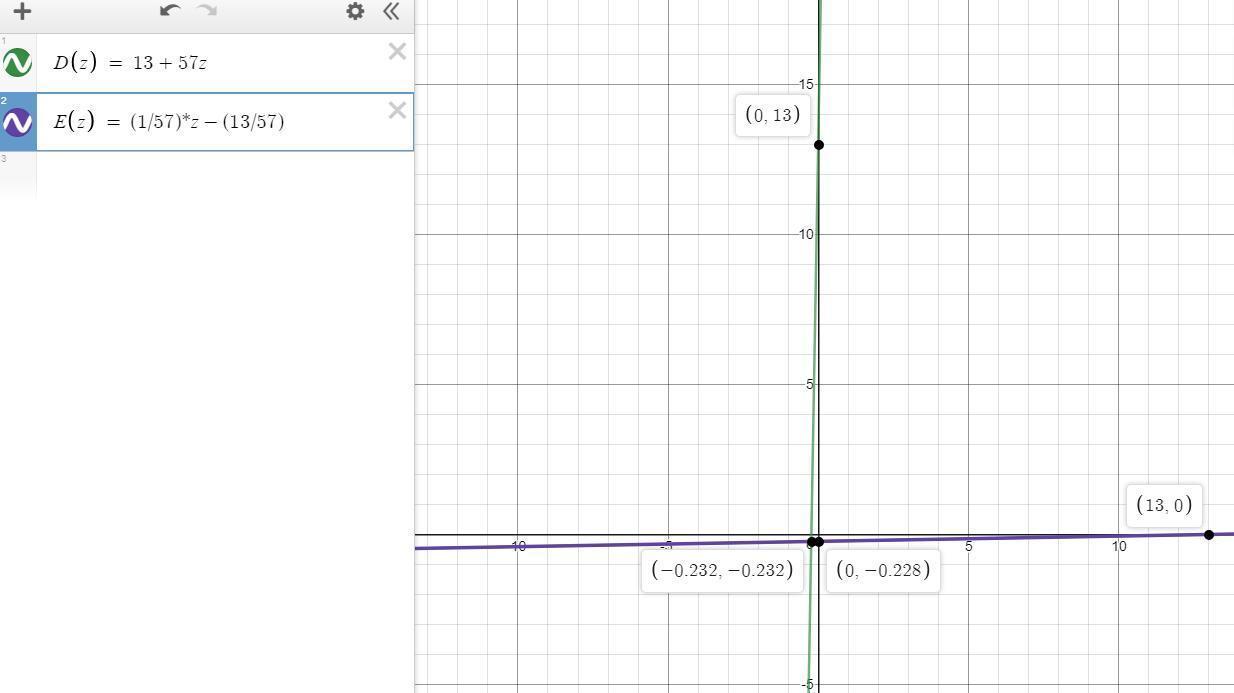
a) t = D^-1(x) = (1/57)*x -(13/57)
b) t = D^-1(x) = 1 h
c) D^-1(x) represents time.
d) The number of hours of driving needed for Sarah to be x km from Tempe. (option (c))
Step-by-step explanation:
a) Determine a formula in terms of x for: t = D^-1(x)
The distance in km from Tempe after t hours of driving is given by
x = D(t) = 13 + 57t.
We just need to find the value t function of x
x = 13 + 57*t
x -13 = 57*t
57*t = x -13
t = (1/57)*x -(13/57)
We can see the plots of both equation in the picture below.
b) Compute D^-1(70)
Once we find the expression for D^-1(x)
We substitute for x = 70 km
t = D^-1(x) = (1/57)*x -(13/57)
t = D^-1(x) = (1/57)*(70) -(13/57)
t = D^-1(x) = (70/57) -(13/57)
t = D^-1(x) = (1.228) -(0.228)
t = D^-1(x) = 1 h
c) In the expression D^-1(x) : what quantity (distance or time) does the x represent? what quantity (distance or time) does the entire D^-1(x) represent?
x represents Distance in both equations (D(t), and D^-1(x))
t represents Time in both equations (D(t), and D^-1(x))
Since t = D^-1(x),
D^-1(x) represents time.
d) Which of the following statements best describes D^-1(x)?
The number of hours of driving needed for Sarah to be x km from Tempe.
Since, t = D^-1(x), and t represents the amount of time elapsed since Sarah, parted from Tempe, the correct answer is option (c)
The expression for D^-1(x) can be found in the previous answers
t = D^-1(x) = (1/57)*x -(13/57)
The input is x (distance) and the output is t (time)
-
Author:
fionaghmi
-
Rate an answer:
2
AI generated Answer
-
Rate an answer:
0
Do you know an answer? Add it here!
Unable to find an answer to your question?
Don't worry! There are several alternative approaches you can try to resolve your query. Here are some tips to help you find answers in different ways:
- Reframe your question: Sometimes, the way you phrase your question can limit your search results. Try rephrasing it using different keywords or providing more context to get better results.
- Utilize social media: Post your question on social media platforms, particularly those focused on professional or specialized topics. Twitter, LinkedIn, and Facebook groups can connect you with individuals who may have relevant expertise or experiences to share.
- Consult subject matter experts: Reach out to experts in the field related to your question. Many professionals are willing to help and share their knowledge. You can connect with them through email, LinkedIn messages, or by attending relevant conferences or events.
- Use our website to find your question through the search box above, or you can sign up to ask your question for our big educational community. Our experts will review your question, and you will get a quick and quality answer.
- Collaborate with others: If your question is related to a specific project or problem, consider collaborating with others who might have complementary skills or knowledge. Teamwork can lead to innovative solutions and shared insights.
Remember, the process of finding answers often involves persistence, creativity, and an open mind. By exploring various resources, reaching out to others, and being proactive in your search, you increase your chances of finding the information you need. Happy quest for knowledge!