Find all the zeros of the equation x^4-6x^2-7x-6=0 Explain please.

• zeros are {-2, 3, (-1±i√3)/2}

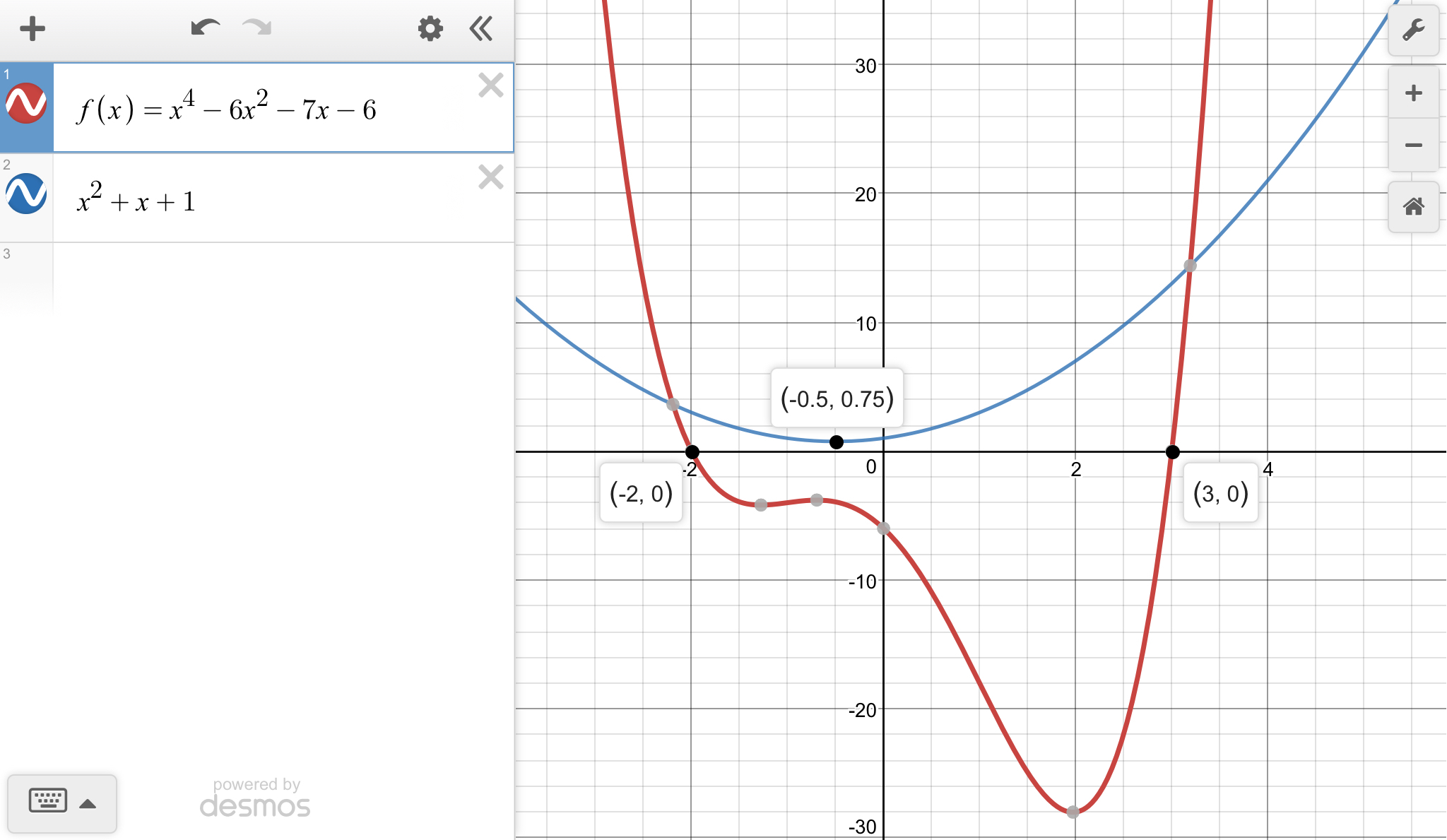
I like to look at a graph of the function to see where the zeros might be. Here, there are x-intercepts at x=-2 and x=3. These can be factored out using synthetic division to find the factorization to be ...

... (x +2)(x -3)(x² +x +1) = 0

By completing the square, using the quadratic formula, or by looking at the graph of it, the complex roots of the quadratic factor can be found to be ...

... x = (-1 ±i√3)/2

_____

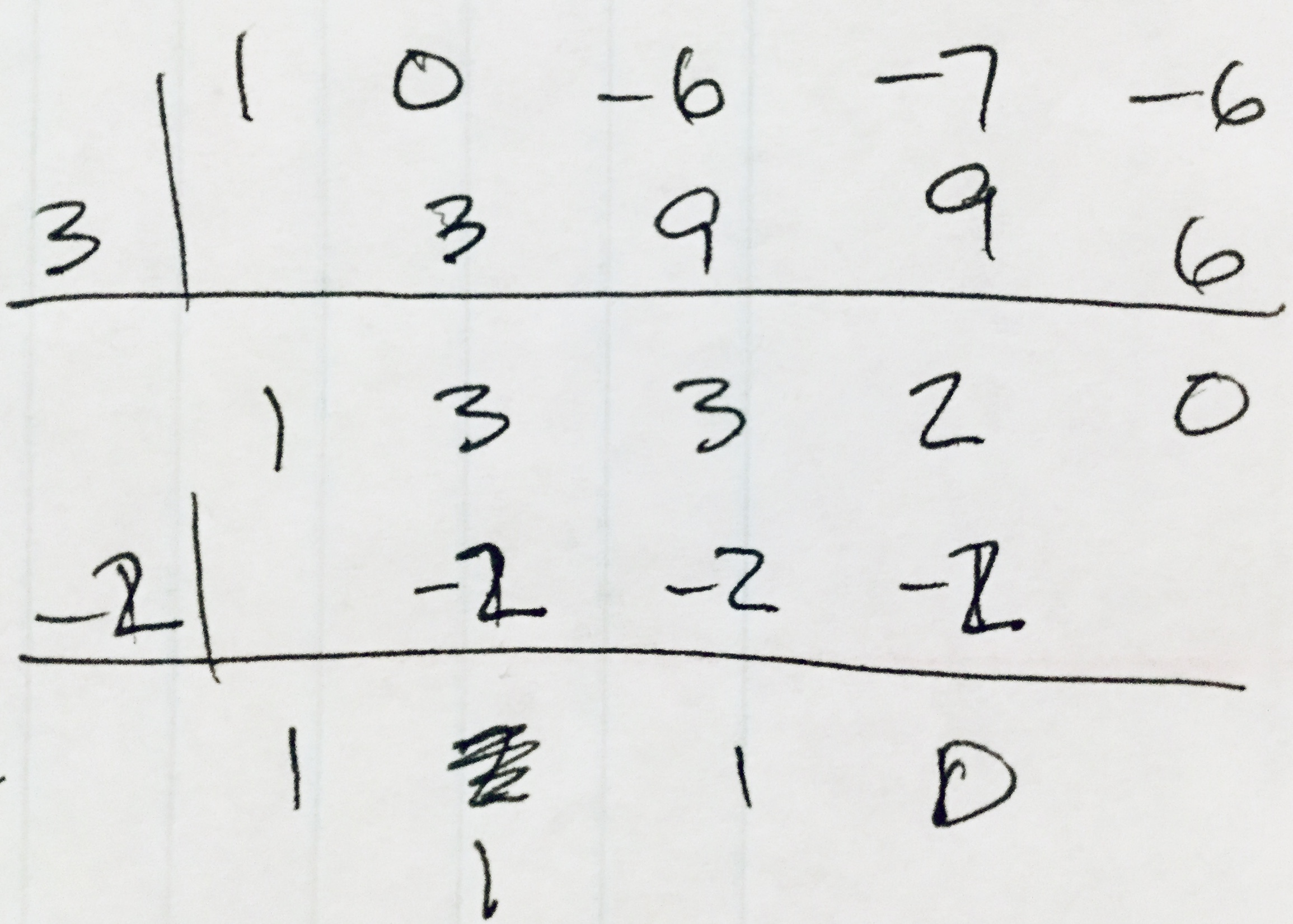
The second attachment shows my synthetic division. The first division takes out the root x=3 to give a quotient of x³ +3x² +3x +2. The second division takes out the root -2 to give the quotient of x² +x +1. (You can see that I tried -1 as a root first.)

The graph shows both the quartic and the quadratic factor of it. The latter has a leading coefficient of 1 and a vertex at (-1/2, 3/4), so you know the complex roots are -1/2 ±i√(3/4).

_____

From the beginning

There is only a very complicated formula for the roots of a quartic equation, so these are usually solved by machine or by some form of trial and error (iteration). There are some helps, like Descarte's Rule of Signs, and the Rational Root theorem.

Here, the former looks at the one sign change in the coefficients to tell you there will be 1 positive real root. Changing the sign of the odd-degree terms makes there be 3 sign changes, so there will be 3 or 1 negative real roots. Thus, we're assured at least two real roots, one of each sign.

We can look at the constant term to find the y-intercept to be -6. We can add the coefficients to find the value of the function is -18 for x=1, so the positive real root is larger than 1.

The Rational Root theorem says any rational roots will be factors of 6, the constant term. Choices are 1, 2, 3, 6. We have already eliminated 1 as a possibility, and we consider it unlikely that 6 will be a root. (The 4th power overwhelms the other terms in the function.) We tried 2 and found it doesn't work (this was before we graphed the function). The attached division result shows that 3 is a root, as does the graph.

Once you get down to a quadratic, you can find the remaining roots in the usual way. Because it is so simple to read them from the graph, we decided to graph the quadratic factor.

_____

Comment on terminology

"root" and "zero" are essentially the same thing when the function is equated to zero, as here. The terms refer to the value(s) of x that make the polynomial function evaluate to zero.